| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- turtlebot
- rosnoetic
- Ros
- Slam
- realtimerendering
- pointcloud
- imageprocessing
- ComputerVision
- electromagnetism
- vectorcalculus
- turtlebot3
- roslaunch
- rospackages
- raspberrypi
- 3dmapping
- NERF
- vectorfields
- adaptivedensitycontrol
- differentiablerendering
- tilebasedrasterizer
- gaussiansplatting
- usbcamera
- LIDAR
- catkinworkspace
- rostopics
- 3dgaussiansplatting
- opencv
- alphablending
- covariancematrix
- sensorfusion
- Today
- Total
Wiredwisdom
Ray for Final Color (Alpha-blending & NeRF) 본문
Ray for Final Color (Alpha-blending & NeRF)
Duke_Ryan 2024. 6. 22. 16:26
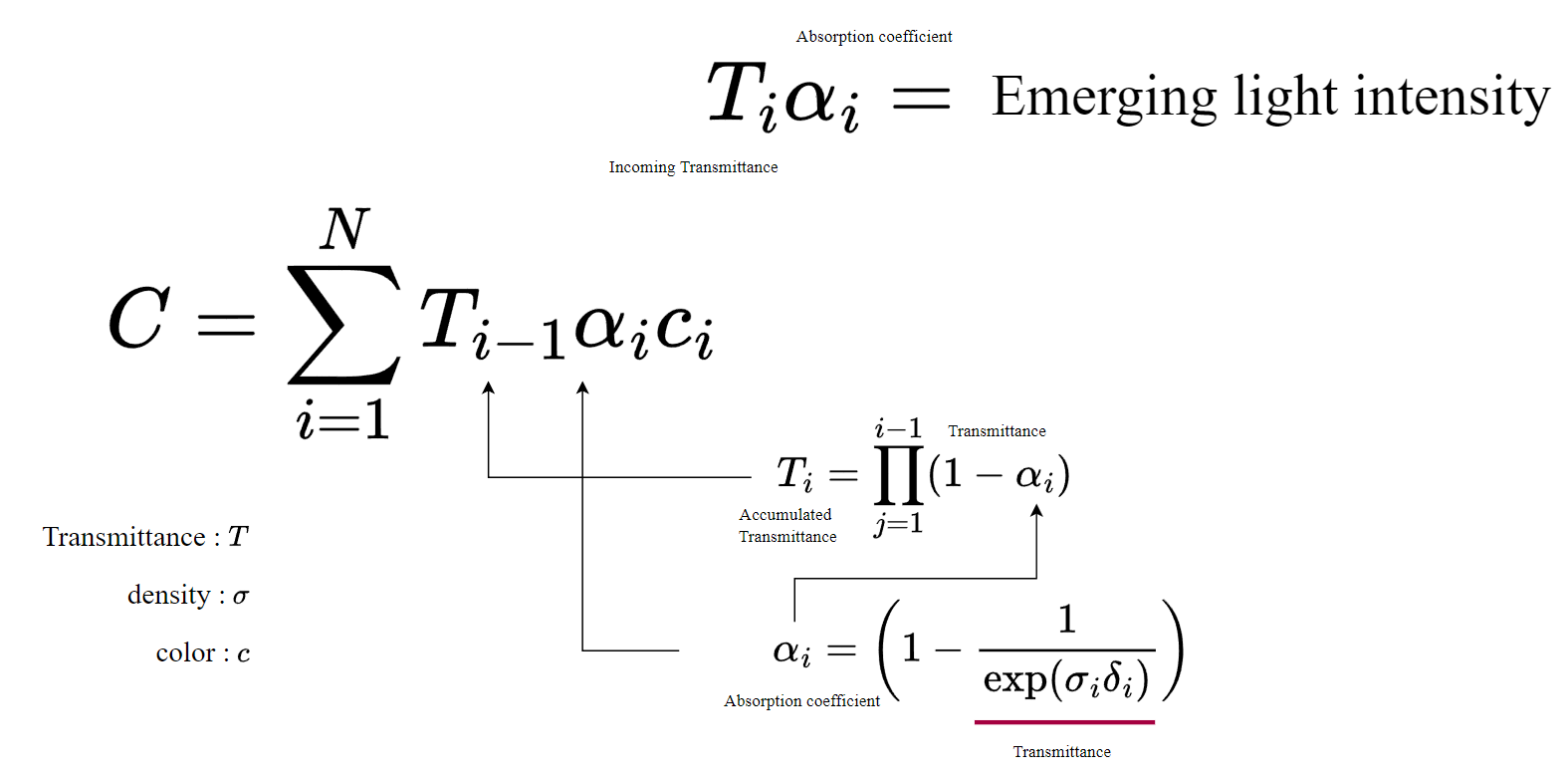
기본적으로 최종 색상은 위와 같이 계산된다.
하지만 여기서 중요한 사실은 해당 가우시안이 포인트의 집합이라는 것이고
첫번째 가우시안에서 발산되는 색상이 뒤의 가우시안을 지나침에 따라 감쇠되는 속성은 계산하지 않았다는 사실이다.
Transmittance와 opacity의 값을 더하면 1이 된다.

각 Transmittance를 적층해서 구하는 식을 그리고 있다.
먼저 각 매질의 Transmittance를 각 매질의 두께(특정 Ray가 지나가는 두께)와 밀도를 통해 exp 함수로 표현하고
여기에 1을 빼어 Opacity를 구한다.
이 값을 가지고 다시 Accumulated 된 Transmittance를 구하게 되는 것이다.
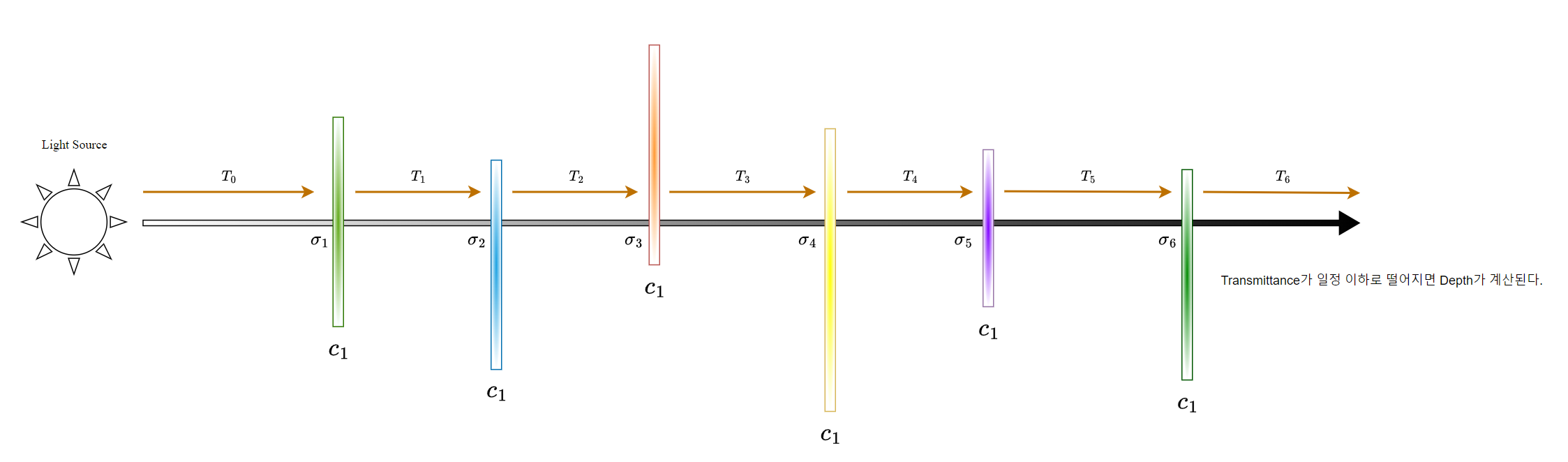
하나의 광원, Ray가 각 가우시안을 투과하면서
최종적으로 Transmittance가 특정 기준점 이하로 떨어지는 때까지의 과정을 그렸다.
이렇게 6개의 가우시안을 지나가게 되는데 마지막 가우시안의 위치가 Depth 이 된다.
여기서는 색상은 고려하지 않고 빛의 투과율만으로 Depth을 구하게 되고
여기서 발산이 되는 색상은 밑의 모델에서 다시 구하게 된다.

본래는 빛이 반대로 빠져나오는 그림을 그려야 하지만,
그렇게 되면 가우시안들의 순서가 뒤바뀌면서 각 가우시안이 점유하는(Accumulated 된 Opacity) 불투명도에 따라
빛의 세기도 달라지게 된다. 즉 색상 조합이 엉키게 되는 것이다.
따라서 계산적 편의성을 위해(실제로 이것이 효과적인지는 모르지만 논문으로는 증명되었다) 빛의 투과는 외부에서 안쪽으로 들어오는 방향으로 계산하고, 마지막 가우시안을 투과하고 나온 빛이 `alpha`-Bleding 된 빛의 최종값으로 나오는 것이다.
그래서 본래의 초록색 픽셀 값은 왼쪽에 그렸고, 최종 계산 값은 오른쪽에 그렸다.
이 픽셀의 차이를 Loss Function으로 하여 각 가우시안을 Depth 이 가장 깊은 곳에서부터 차례대로 Chainrule로서 계산을 하게 되면 각 가우시안이 가지는 색상과 불투명도에 대한 기울기를 산출할 수 있게 되는 것이다.
아래는 Color와 Opacity에 대한 각 가우시안의 기울기를 구하는 식이다.
이 기울기를 통해 Learning rate를 통하여 Color와 Opacity 를 매 학습시마다 변화를 준다.

논문에서 설명된 최종 적층된 `alpha` 값 만으로 각각의 가우시안의 적층 값을 산출하는 식이다.
이는 메모리 점유율을 줄이기 위한 테크닉이다.
여기서의 `T_(i-1)`은 위의 `(delC)/(delc,alpha)` 에서 활용이 된다.

계산되는 모습을 그림으로 표현했다.
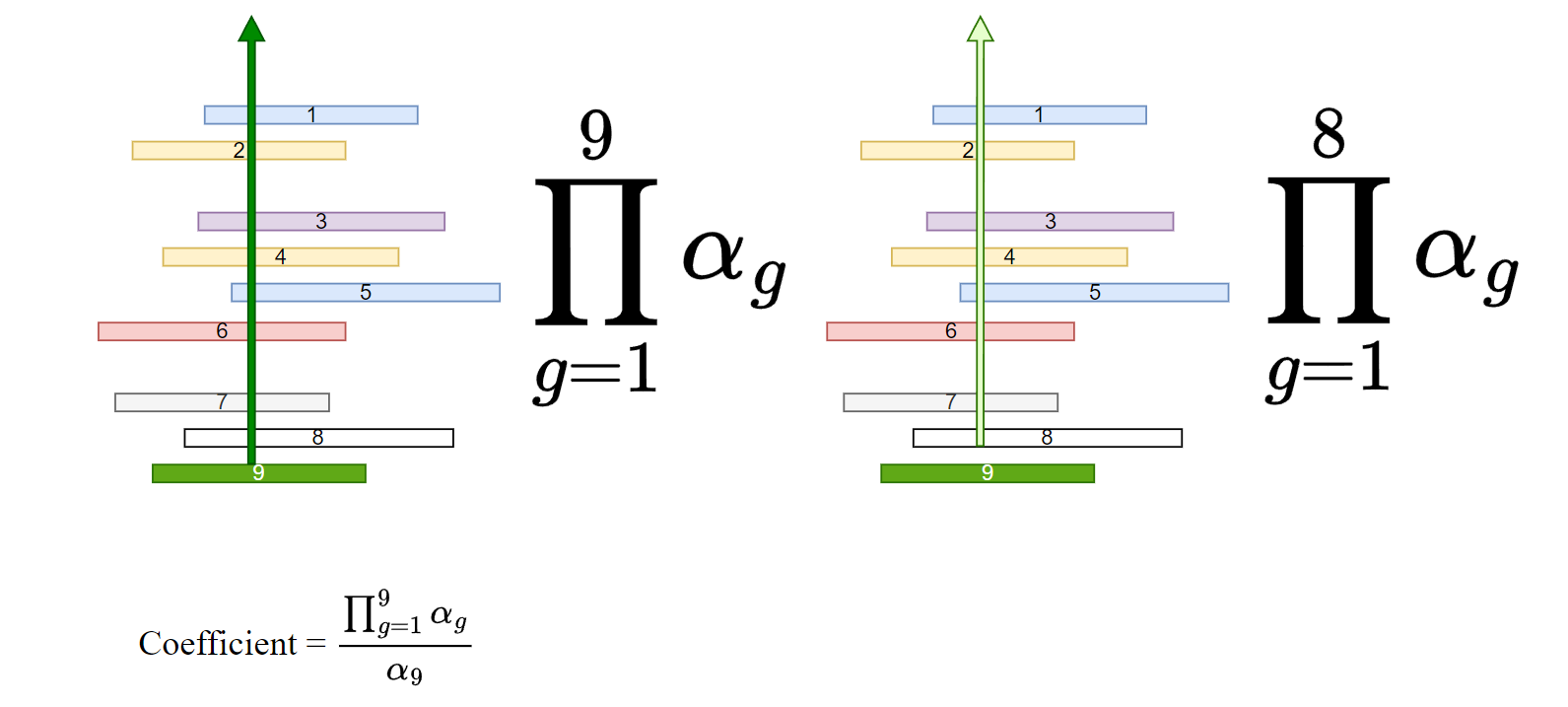
즉 논문에서 표현하는 coefficient 는 각 가우시안의 Accumulated 된 aplha 값이 된다.
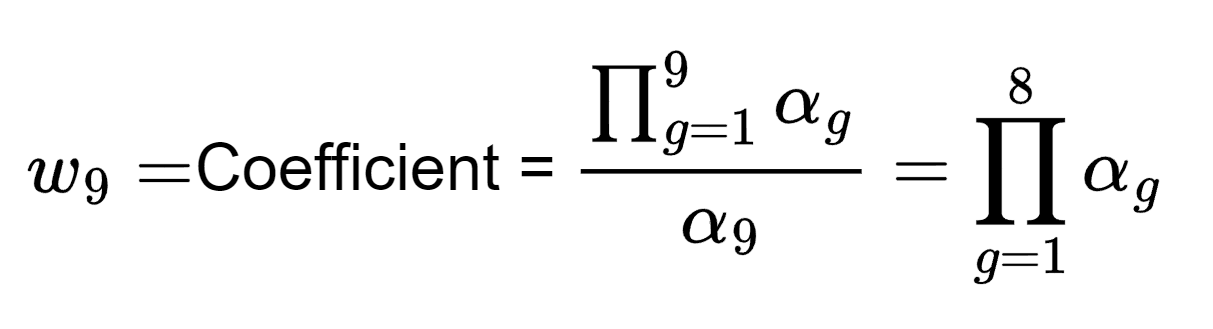
정리해보자.
각 매질 마다 순차적으로 들어온 빛의 흡수정도에 따라 색상을 계수로 곱해주어 비중을 만들어주고,
각각의 가우시안의 흡수율을 해당 색상과 곱한 값 값들을 모두 더하여 최종적인 색상의 구성을 출력(표현)한다.
Transmittance는 최고값이 1이기 때문에 들어온 빛의 비율로 해석하고,
각 매질별로 빛이 분배가 되어 최종적인 색상이 결정되는 것으로 이해하면 된다.
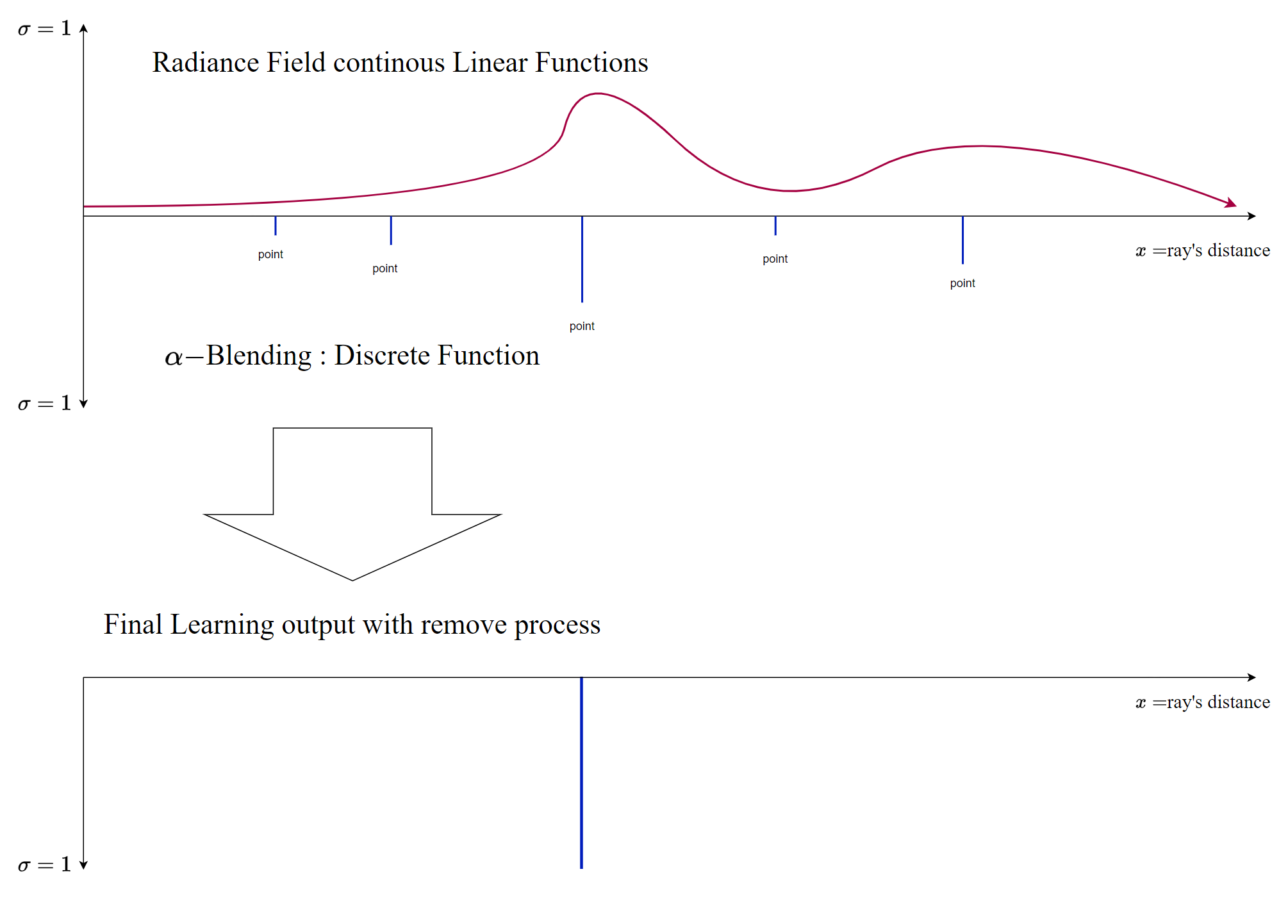
NeRF의 Radiance Field는 특정 광원을 MLP를 통해 Continous 하고 Linear 한 함수로 표현한다.
그러나 `alpha`-blending의 경우는 이산적이며 최종적으로는 하나의 포지션에 밀도가 1로 표기될때까지 학습을 반복한다.
반투명한 물체는 없다고 보는 것이다. 대신 포인트를 무수히 미세한 점으로 보지 않고 3D-Gaussian을 스플랫으로 활용하여 공간을 점유시키고 해당 부피를 확장하거나 쪼개는 방식으로 이루어진다.
둘다 형태는 다르지만 미분이 가능한 접근 방식이며
때문에 Back Propagation으로 Loss-function의 기울기를 산출 할 수 있다.
'3D Vision > Gaussian Splatting' 카테고리의 다른 글
| 3D Gaussian-Covariance (0) | 2024.07.03 |
|---|---|
| FAST DIFFERENTIABLE RASTERIZER FOR GAUSSIANS (0) | 2024.06.30 |
| Convert 3D Gaussian to 2D splat Method (0) | 2024.06.22 |
| Overview (0) | 2024.06.22 |
| Gaussian Splatting (0) | 2024.06.21 |




