| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- geometrylearning #shapeoptimization #gpuacceleration #realtimerendering
- gaussiansplatting #3dgaussiansplatting #pointbasedrendering
- realtimerendering #highquality3d #fastrendering
- differentiablerendering #machinelearning3d #deeplearninggraphics
- anisotropickernels #ellipsoidalsplatting #orientedsplats #gradientbasedlearning
- computergraphics #3dmodeling #virtualreality #augmentedreality #gamedevelopment
- nerf (neural radiance fields) #3dreconstruction #pointcloudrendering #volumerendering
- 3dscanning #digitaltwintechnology #3dcontentcreation
- splatrendering #3dpointcloud #differentiablerendering
- pointbasedrendering #computergraphics #3dmodeling #volumerendering
- turtlebot3 #터틀봇
- 3drenderingtools #pointcloudsoftware #3dvisualizationsoftware
- machinelearning3d #deeplearninggraphics #airendering
- nextgengraphics #futureof3drendering #innovativerenderingtechniques
- 3dscenerepresentation #covariancematrixoptimization #adaptivegaussians
- computervisionresearch #3dreconstructiontechniques #graphicsresearch
- gpuacceleration #aigraphics #virtualreality #augmentedreality #gamedevelopment
- realtimerendering #machinelearning3d #deeplearninggraphics #computervision
- anisotropicgaussianlearning #gaussiansplatting #nonisotropicrenderinㅎ
- advancedrenderingtechniques #neuralscenerepresentation
- 3dsceneunderstanding #pointcloudrendering #neuralscenerepresentation
- siggraphtechniques #aigraphics #3dmodelingalgorithms
- siggraph #3dsceneunderstanding #highquality3drendering #fastrendering
- optimizationalgorithms
- highfidelityreconstruction #sceneunderstanding #computationalgraphics
- 3dpointcloud #differentiablerendering #3dscenerepresentation #neuralrendering
- gaussiansplatting #3dgaussiancovariance #nerf #3dreconstruction
- nerf (neural radiance fields) #3dreconstruction
- gaussianprojection #covariancematrix3d #anisotropicgaussians #ellipsoidalsplatting
- 3dcontentcreation
- Today
- Total
Wiredwisdom
3D Gaussian-Covariance 본문
2D의 가우시안의 평균이 원점인 경우를 보자.
여기서 Covariance가 0인 경우는 다음과 같은 타원형이 된다.
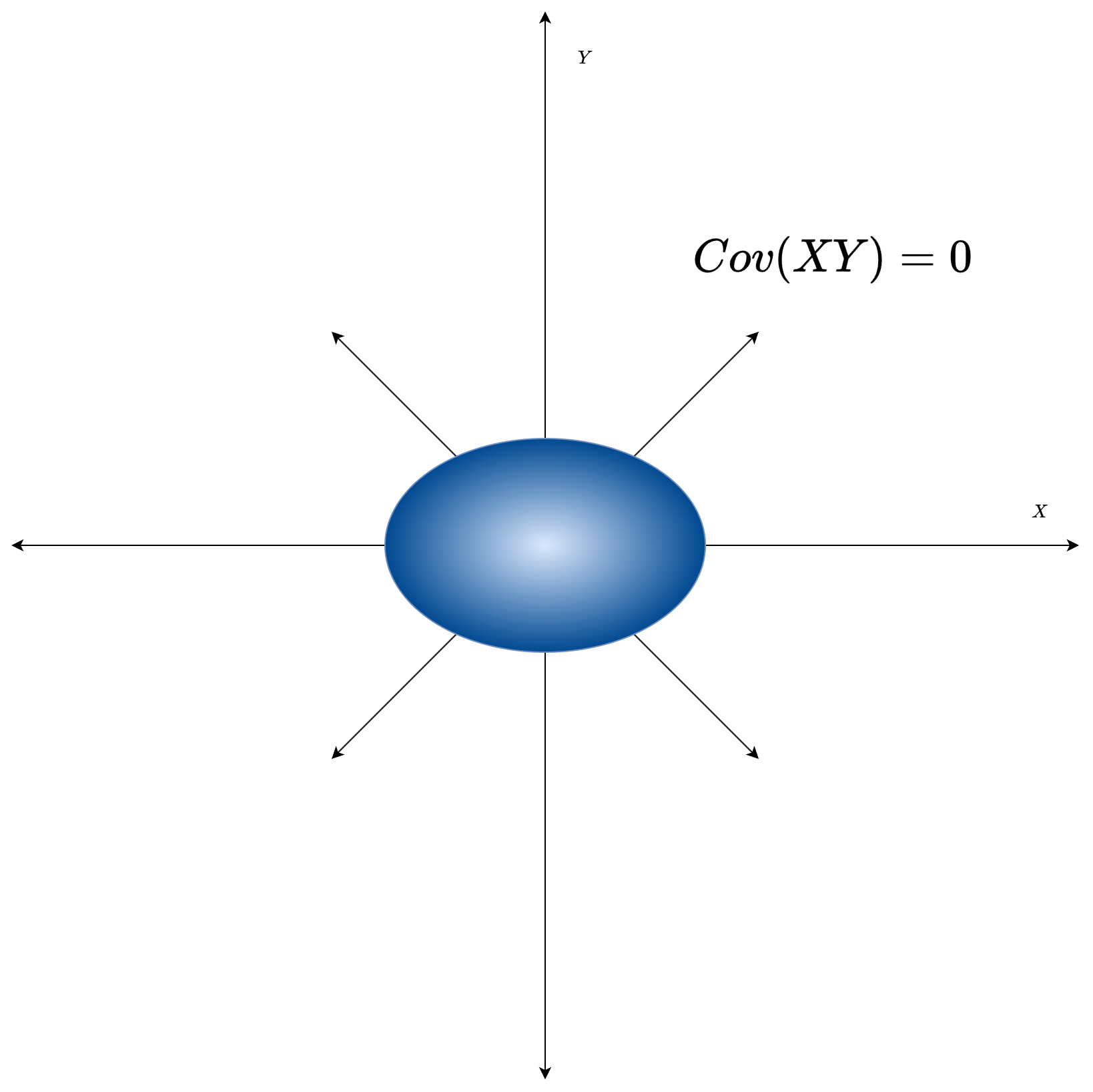
Covariance가 0 보다 크게 되면 다음과 같은 값을 갖게 된다.
1,3 사분면으로 분포도가 두드러지며, 2,4분면은 상대적으로 납짝해진다.

Covariance 가 0보다 작은 경우는 2,4 분면으로 분포가 두드러지고
1,3분면은 반대로 납짝해진다.

이를 통해 알 수 있는 것은 Covariance가 가우시안의 모양을 나타내는 주요 인자로 작용한다는 의미이다.
그러나 이 Covariance가 분포의 양과 음의 값과, 그 길이를 나타낼 수는 있어도
분포도가 가지는 선형성의 기울기를 알 순 없다.
그 기울기에 대한 정보는 Covariance Matrix의 대각행렬이 갖는다.
`[(x x,xy),(yx,yy)]`
에서 대각행렬을 Scale이라 하고
아래 그림과 같이 각 축방향으로의 공분산의 길이를 의미하는데
여기서 기울기가 산출이 된다.
양과 음의 값과 가우시안 그래프가 뚱뚱한 정도는 Covariance가 담당하는 방식이다.

그리고 Gaussian Splatting에서 Covariance Matrix `(3xx3)`에서는
비대각행렬을 0으로 처리하는데
위의 가우시안에서 비대각 행렬을 0으로 처리하면 아래와 같이 가우시안의 형태가 변형된다.
이 형태를 Rotaion하여 2D 단면의 Gaussian을 도출하고
해당 2D Gaussian들을 가지고 `alpha`-bleding을 시작한다.

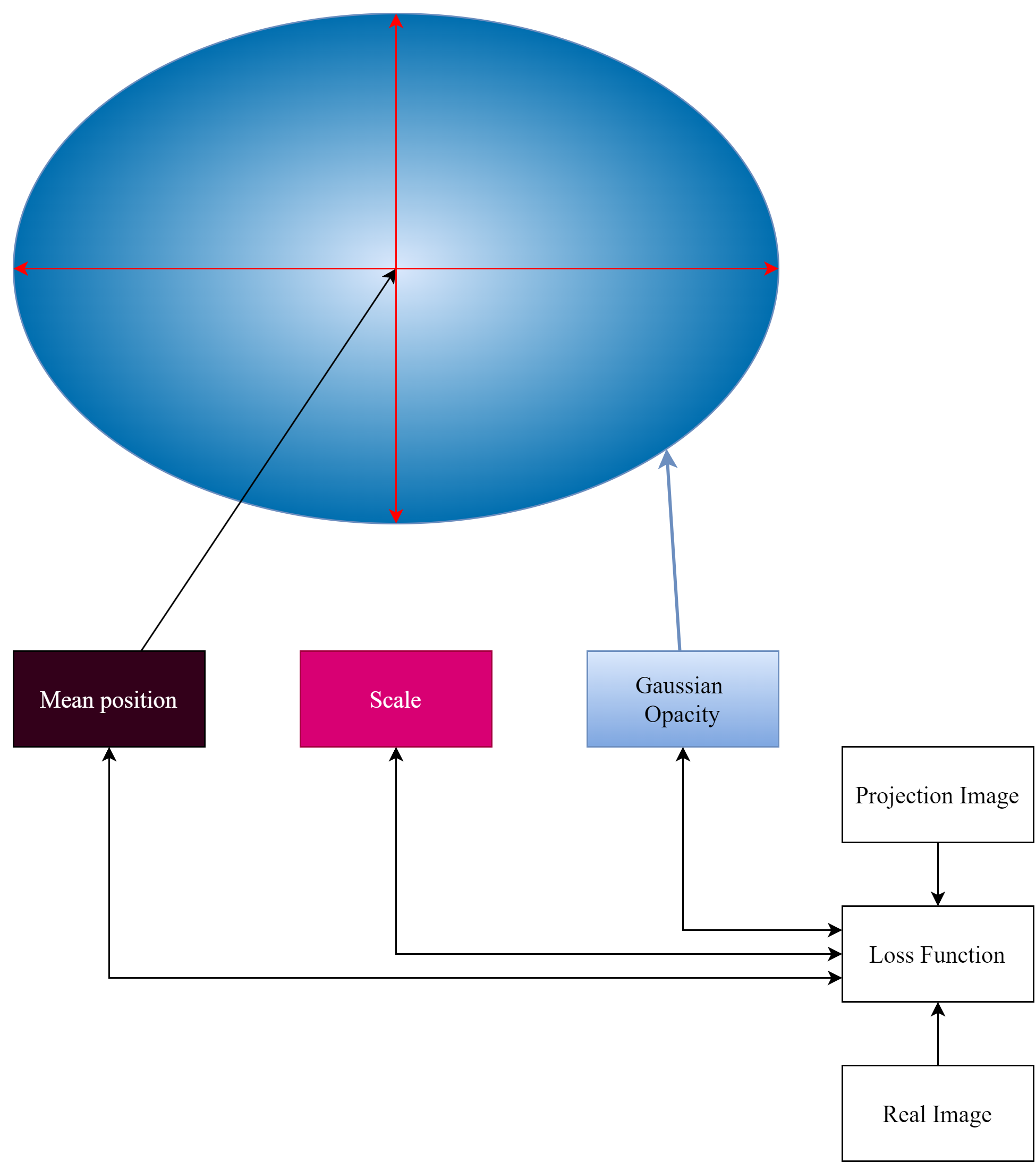
그리고 학습은 다음과 같이 이루어진다.
Loss Function을 토대로 각 가우시안들의 중심값의 이동여부와
Scale의 확장 축소 여부
그리고 각 가우시안이 가지는 Opacity에 대한 레벨이 그것이다.
하나의 가우시안이 Opacity 가 1인, 즉 빛이 투과되지 못하는 완전히 불투명한 물질을 표현할 수 있다.
그러기 위해서는 가우시안의 Opacity 정도와 가우시안의 중심으로 갈 수록 높아지는 밀도가 동시에 관여되어야 한다.
이는 대체로 Pixel단위로 가우시안이 작게 분할되었을때 (충분히 학습되었을때) 이루어지는 것으로 보여진다.
'Vision > Gaussian Splatting' 카테고리의 다른 글
| 가우시안 스플래팅의 비등방성 학습 해결 방안 (0) | 2024.07.10 |
|---|---|
| 3D Gaussian's Split conditions (0) | 2024.07.04 |
| FAST DIFFERENTIABLE RASTERIZER FOR GAUSSIANS (0) | 2024.06.30 |
| Convert 3D Gaussian to 2D splat Method (0) | 2024.06.22 |
| Overview (0) | 2024.06.22 |



